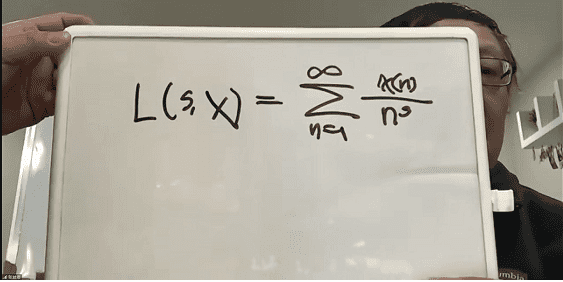
On November 8, at an academic presentation organized by the School of Mathematical Sciences of Peking University (PKU), Yitang Zhang shared his thoughts and methods on solving the Landau-Siegel zeros problem and explained his latest results to PKU faculty, students, and the public.
Previously, on November 4, his paper on the Landau-Siegel Zeros Conjecture, “Discrete mean estimates and the Landau-Siegel zero”, was officially uploaded to the preprint site arXiv.
Yitang Zhang, a Chinese-American mathematician who is currently a professor at the University of California, Santa Barbara, says that the research results only prove to a small extent that the Landau-Siegel zero conjecture is correct, i.e., that this zero may not exist.
In 1859, the German mathematician Bornhard Riemann had proposed the Riemann ζ-function and the Riemann hypothesis that the zeros (function values equal to 0) of this function all correspond to the real part of the function equal to 1/2.
That is, if the real part is greater than 1/2, this function is not equal to 0.
Later, based on the Dirichlet L-function (Dirichlet L-function, a discontinuous function defined on the real range), Edmund Landau and Carl Siegel found that a special class of L-functions may have an abnormal zero (exceptional zero).
If this zero exists (called the Landau-Siegel zero), the generalized Riemann hypothesis is wrong.
And the Landau-Siegel zero conjecture holds that there is no such zero.